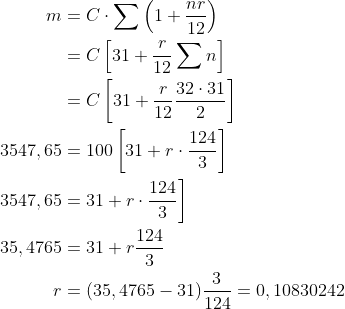vurvujo
Madmaxista
- Desde
- 10 Abr 2018
- Mensajes
- 11.706
- Reputación
- 21.631
En capitalización simple el 11,30928% y en compuesta el 10,35669%
¿Cómo obtuviste esos números?.
No estoy seguro que en una inversión tenga los mismos cálculos de tasas pactadas.
Follow along with the video below to see how to install our site as a web app on your home screen.
Nota: This feature may not be available in some browsers.
En capitalización simple el 11,30928% y en compuesta el 10,35669%
Tendría¿Cuánto te da según lo que aprendiste en bachillerato?
la fórmula es¿Cuánto te da según lo que aprendiste en bachillerato?
Tendría
la fórmula es
C= a(1+r) ((1+r)**t-1))/r
r tasa mensual
C capital final
a cantidad mensual
t tiempo en meses
Al resolver en r sale,
Lo tengo que hacer en el ordenador
A ojo estará entre 5-6% al año
Me da 0,86305% mensual aprox 10,3% anual¿Y cuantó te da? en indicativo.
Me da 0,86305% mensual aprox 10,3% anual
Ver archivo adjunto 1771859
En C1 =TIR.NO.PER(A1:A32;B1:B32)
En D1 =TASA(31;-100;0;3567,45;1)
En D2 =POTENCIA(D1+1;12)-1
Con ambas funciones da el mismo resultado, le veo sentido a ambas funciones, imagino que debe ser correcta.
No conocía la función TIR.NO.PER... muy útil.
Si, es la diferencia entre tir, tae, etcLo que dijo Aceite de Ojiva 0,86% mensual.
Lo que sí es que tienes que revisar la conversión de tasas, porque no es simplemente *12, sino del tipo r'= (1+r)^12-1
Fórmula de anualidades de capitalización, incógnita la tasa de interes
Se estudiaba en bachillerato antaño
Pues a mi me lo ensañaron en bachillerato, probablemente con 14 añosEso es como magia de alto nivel.
Casi todos los diplomados o como se llame ahora de Económicas salen con el título debajo del brazo sin saber convertir una tasa de interés simple en compuesto (o al revés), o a cuánto corresponde si el pago de intereses se hace bimensual, trimestral u otro cualquier periodo.
A cualquier político patrio si le hablas en taiwanés te endiende mejor que si le explicas esto.
Ese seria el calculo para una aportación única inicial de 3100.Supongo que no es la manera correcta pero a mi me sale lo siguiente:
Mensualmente: 0,45%
=((3567,45/3100)^(1/31))-1
Anualmente: 5,59%
=(((3567,45/3100)^(1/31))^12)-1
Las ecuaciones son:
n = 31
3.547,65 = 100 x Ʃ (1 + (n x 0,1130928/12)) para la capitalización simple
n = 1
n = 31
3.547,65 = 100 x Ʃ (1 + 0,1035669/12)^n
n = 1
¿Pero lo hiciste iterando? Para poder resolver la tasa de interés de una sumatoria no se hace tan fácil.
Exacto, mediante un algoritmo de prueba y error
Imagino que en la primera ecuación el término de la sumatoria debería estar elevada a la n o algo así, porque no me da.
Los términos sería (en capitalización simple):
[(1 + 0,1130928/12) + (1 + 2 x 0,1130928/12) + .......... + (1 + 31 x 0,1130928/12)] x100 = 3.567,45
(1,0094244 + 1,0188488 + ................................+ 1,2921564) x100 = 3.567,45